優化演算法練習 Leetcode X Bitwise Operators 介紹

Posted on Edited on In ,
Leetcode X Bitwise Operators
Leetcode X Bitwise Operators
Leetcode X Bitwise Operators
．．．

想當初剛進入資策會學的第一堂 Javascript 課就是在教二進制運算符 Bitwise Operators，但當初老師林林總總畫了一堆表伴隨了滿課堂的疑惑聲至今仍許多人沒有帶走老師的一片雲彩．．．

進入前端產業也三年了不懂好像說不過去，趁這次練習 Leetcode 某一個倒讚多到不行的神奇題目好好學起來 XD
這題可以說總結了二進制學習的兩大精華：XOR ^ 運算符與 AND & 運算符的魔法:

拆解題目

  1. Sum of Two Integers (Medium)
    Given two integers a and b, return the sum of the two integers without using the operators + and -.

  • Example 1:

    Input: a = 1, b = 2
    Output: 3
    Example 2:

  • Example 2:

    Input: a = 2, b = 3
    Output: 5

  • Constraints:

    -1000 <= a, b <= 1000

這題非常特別，在不使用 operators + and - 情況下計算 a and b 總和，想必有什麼特殊魔法吧！
「咻咻咻咻－－」二元運算法！

超棒影片推薦

對文組人非常友善的影片介紹：

影片內提及運算法的幾個重點：

XOR 二元或、異位元運算法 (Exclusive or)

將十進制換算成二進制之後就可以先透過 XOR 模擬加法運算，但此法不夠完善的地方在於：
沒有包含進位 但可以先進行第一論的非進位運算，所以我們挪到第二步完成。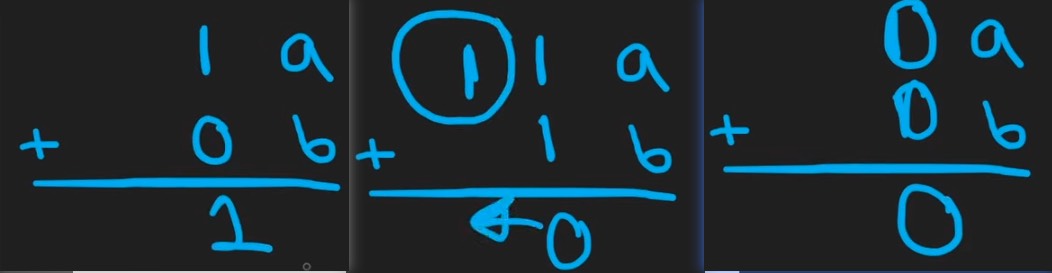

如何轉換十進制為二進制

將數字除以 2 後取得商數以及餘數，持續以新的商數除以 2 後取得新的商數以及餘數．．．以此類推，最後以倒敘方式將餘數記錄下來就會得到二進制的數字：

為什麼第一步採用 XOR

在二次元世界裡就只有 0, 1，而 XOR 對二進制的運算恰巧符合 + 法的運算邏輯：

x y x ^ y
0 0 0
0 1 1
1 0 1
1 1 0

0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 0

最後一行 1 ^ 1 涉及進位所以挪至第二步來計算，

為什麼使用 AND 計算進位 Carry

在二次元世界裡就只有 0, 1，而 AND 對二進制的運算恰巧符合 1 + 1 二元制進位的運算邏輯：

x y x & y
0 0 0
0 1 0
1 0 0
1 1 1

繪製計算邏輯與過程

用範例 9 + 11 以及 8 + 15 來記錄演算法推演過程：

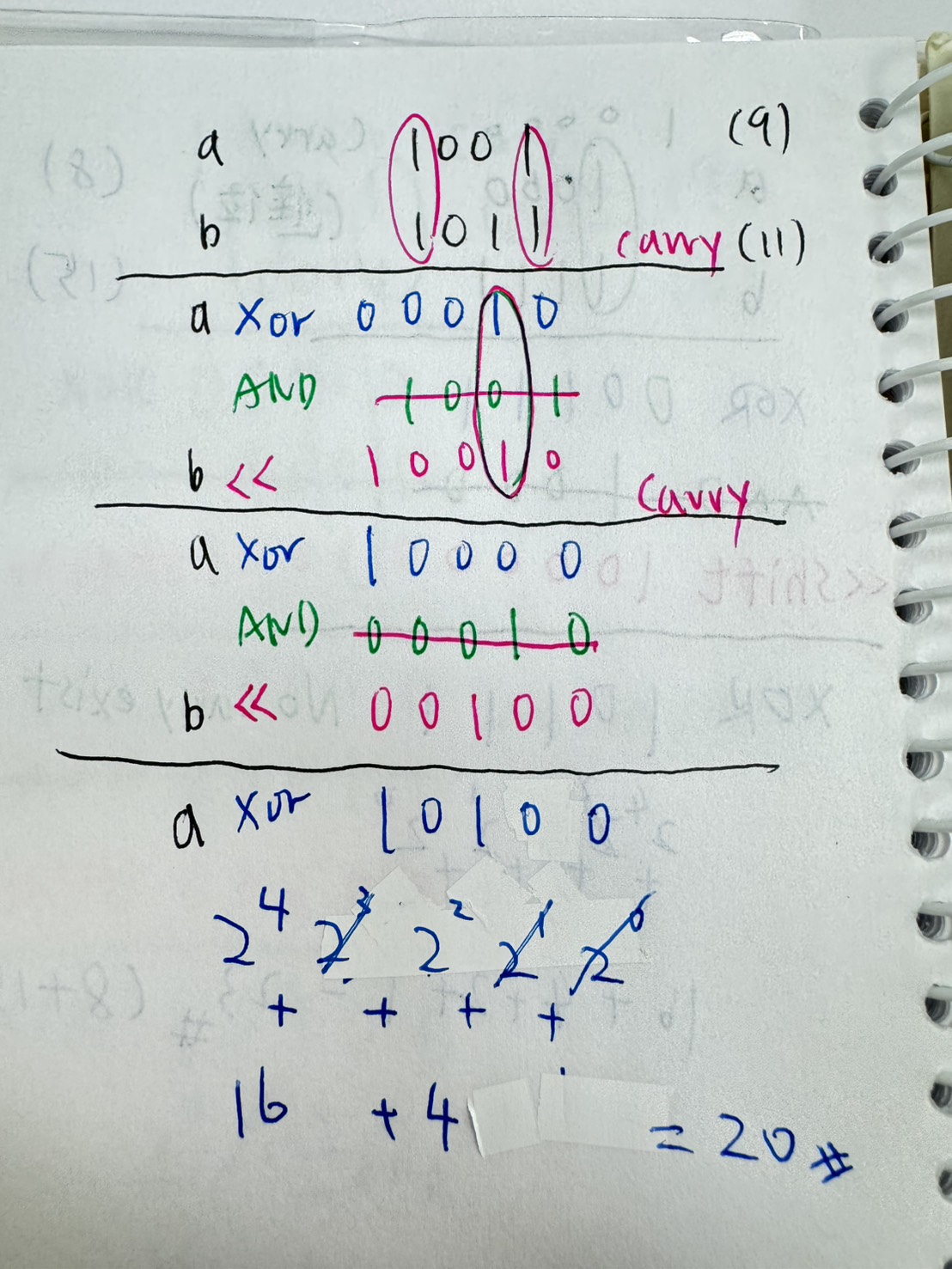
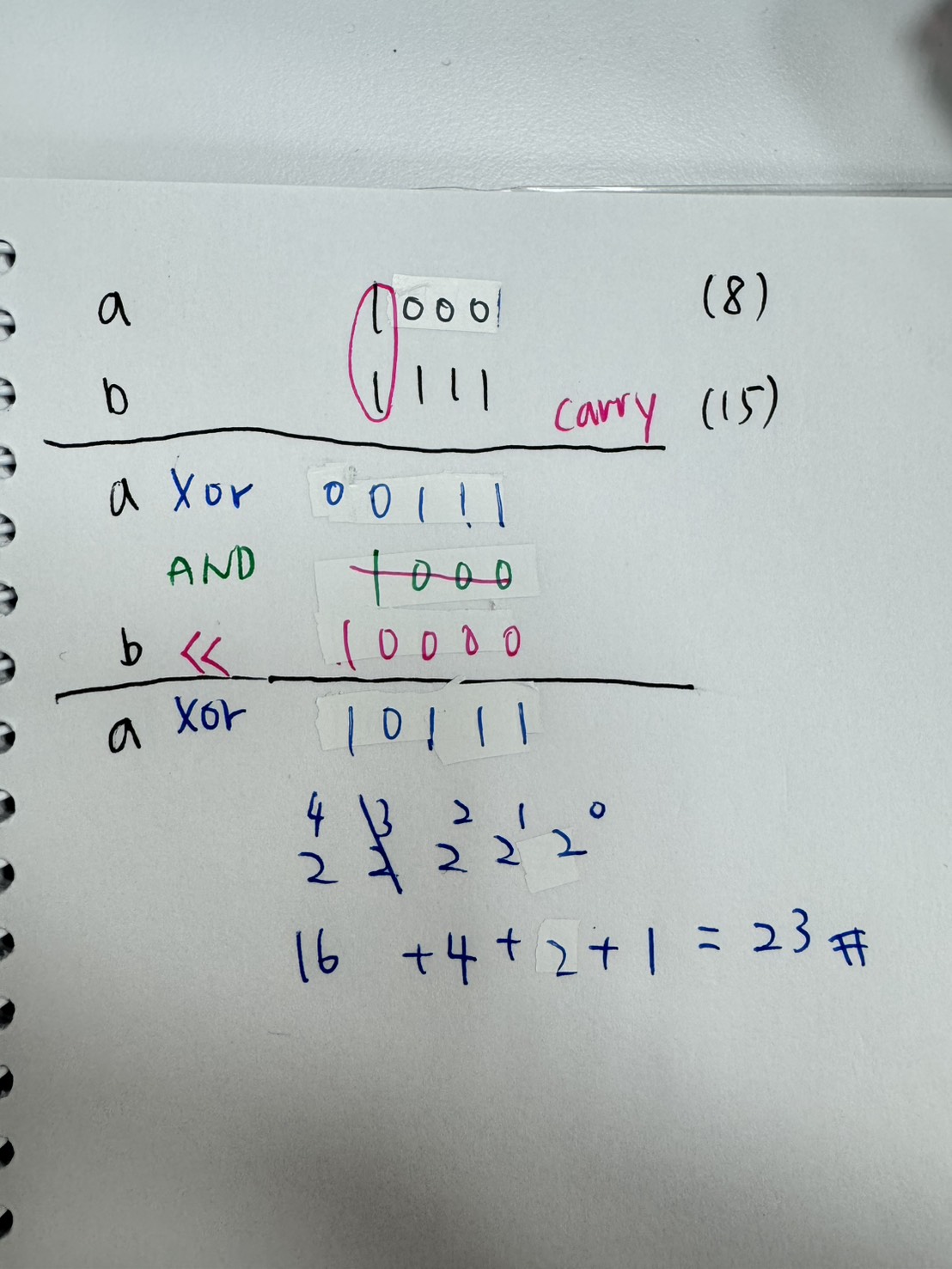
leetcode 演算法

1
2
3
4
5
6
7
8
9
var twoSumWithoutPlusOperator = (a, b) => {
  while (b != 0) {
    let xorAB = a ^ b;
    let carry = (a & b) << 1;
    a = xorAB;
    b = carry;
  }
  return a;
};

  1. 計算上一次 a ^ b 的非進位和，並更新為 a 的值。

  2. 計算溢出的 a & b 進位是等於 1 為 true 的位置，一旦當前運算出現兩個 1 疊加就需要進一步的Carry（進位），處理 XOR 不包含的邏輯部分。

  3. 將 (a & b) 結果執行 << 1 Shift 進位。

    1
    2
    3
    4
    5
    6
    // Adding 3 + 4
    a = 3; // 011 (binary)
    b = 4; // 100 (binary)

    a & b = 011 & 100 = 000  // 計算後確認無進位 position
    (a & b) << 1 = 000 << 1 = 000 // carry 為 0 不需進位
    1
    2
    3
    4
    5
    6
    // Adding 2 + 3
    a = 2; // 010 (binary)
    b = 3; // 011 (binary)

    a & b = 010 & 011 = 010  // 取得進位值 position
    (a & b) << 1 = 010 << 1 = 100  // 將位置往左移一格 010 -> 100

    最後一輪在計算出無任何進位值後就返回 a 的值，可以視為最後一輪的 XOR 加法運算。

題後心得

以上落幕了這題倒讚數很多的題目 XD，順便分享大家對題目的想法：
雖然出題方式偏奇淫技巧也不失為一種有趣的經驗，順便撿回幾年前在資策會遺失的學分也是不錯滴！也不用再下次看見 XOR / AND 兄弟會感到陌生害怕。

（看得出來這位同學怨念很深）